In reading “Talent Management Success: How A ‘Best to Work For’ Company Makes and Keeps Its Employees Happy” on Beth Miller’s Executive Velocity blog, I was intrigued by the fact that PBD, the company in question, sought to develop talent across their whole enterprise through a “best fit” process.
My interest came about because the approach depicted was applicable to all employees rather than what we might call “the chosen few”, which seems to be a talent management theme these days, encouraging organizations to focus on their “A-Players”, “High Potentials”, or “Superstars”.
The Problem with the “Chosen Few” Approach
Conceptually, there are some problems with the “chosen few” approach.
· First, as noted in “5 Reasons NOT to Use the Olympics for Business Lessons”, any organization of a respectable size is quite unlikely to have an entire staff of these folks. If every company in the world is pursuing these folks, and A-players represent 5% of the workforce (if that), the odds are quite long that your firm will be the one they all gravitate towards.
· Second, all employees notice when you are showering the bulk of the attention and other organizational goodies (training, promotions, recognitions, etc.) on a select minority, and this impacts morale, and ultimately you may find that your team has become the microcosm equivalent of “Occupy Wall Street”!
· Third, if A-players represent 5% of our workforce, then it seems to me that their advantage needs to be really great in order to overcome efforts to develop the other 95%. If we can improve 95% of the people by 1%, then devoting our resources to the A-player crew needs to generate a return 19 times greater than that to break-even. Odds of 19:1 seem pretty long. Can their contribution really be that consistently great?
The Search Begins
The breakeven concept introduced in the third point above suggests that if we have an equation for employee talent that factors in both the employee and leader elements then we can analyze whether this 19 to 1 breakeven ratio is reasonable to assume.
For that reason we go looking for the Talent Equation.
The Knowledge Worker Formula
In “Wikifinance, Wikitreasury – Part 2“, an early Treasury Café post, we discussed that the Finance and Treasury role consists primarily of knowledge work. For this reason formulas related to knowledge worker productivity are of interest.
 |
| Figure A |
This is great from an “identify the important factor” viewpoint, but in terms of deploying this in practice several issues arise. What numbers are we to use? Let’s say all factors (i.e. M,T and K) are scored on a scale of 1 to 10. Then KWP would equal 1000 at its maximum, and 0 at its minimum. What does 1000 actually mean in terms of productivity? Five projects get done per day? Five per week? The results are not intuitive.
Another problem we face is that there does not appear to be any role for leadership or other management activities in the equation. M, T, and K can remain the same whether one has a great leader or a lousy one, and under this equation the worker will be equally productive under each. This makes the equation as it stands difficult to use for our break-even purposes.
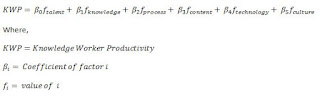 |
| Figure B |
A positive in this equation is that there are leader-related items such as culture and potentially process (depending on the process we are discussing).
However, if the meaning of numbers in the first KWP formula were not intuitive, in this equation it is even more problematic because each term has two numbers, the coefficient (the β item) and the value of the factor itself (the f item). How are these to be determined? And again, what is the value of the result?
Success and Talent Formulas
Striking out in the Knowledge Worker Productivity realm, we turn to more general models. A number of formulas seek to depict success or talent for anyone.
From FarrellWorlds, we have:
Success = Talent + Dedication + Passion + Luck
And from Nilofer Merchant:
S(uccess) = P(urpose)T(alent)C(ulture)
As in the last section, these models are useful from the perspective of answering “what elements are important to consider” issues. However, for our break-even purposes these formulas share measurement problems - ask two people what “success” is and you will get two different answers.
The Per-Person Productivity Formula
One general model that holds a little more promise is one from Derek Irvine, who provides a formula that is heavy on management intervention:
Per-person productivity = Talent x (Relationship +Right Expectation + Recognition/Reward)
Talent is the individual employee’s factor, and the three terms in parentheses relate to the leadership functions.
Let’s assume that Talent is measured on a scale of 0 to 100. For the leadership factors, the critical number for the sum of these is 1. At points higher than this number, Per-Person Productivity improves from their base talent level. At points less than one, it declines.
 |
| Figure C |
The second column (II stands for “Individual Improvement”) is the scenario where we intervene by increasing everyone’s talent by 10%.
The final column (L stands for “Leader”) is the scenario where we improve the leadership factors by 10%, presumably by obtaining some of these A-Players.
The results of each intervention increase the firm’s total productivity from its base case level by 10%. This result is inherent in the equation, since both terms multiply together they will always increase the same percentage amount no matter which term you trigger.
However, what might result from this is that there might be a cost benefit factor which can be used to determine which approach is better. If the Individual Improvement action costs ²100 (for new readers, the symbol ² stands for Treasury Café Monetary Units, or TCMU’s, freely exchangeable at any rate into any currency you choose), then each unit of improvement cost us ²2.
In order to arrive at an “apples to apples” comparison, we need to be careful, as the concept of time enters into this analysis in two ways.
· For the Individual Intervention scenario, if we assume the ²100 is a skills training cost, while this might be a one-time event, its effects will not last forever since workers eventually move on to other positions, win the lottery, retire etc.
· For the leadership scenario, we will need to pay our new A-Player a salary each and every year, so we need to factor in a stream of payments over time and relate that back to one single figure now.
 |
| Figure D |
Under these conditions, we are slightly better off going the A-Player route as the NPV is a little more than ²93, compared to ²100 for the Individual Improvement scenario.
While we successfully completed a break-even calculation using this equation, there are still 2 problems:
· The output of the equation (e.g. 50 and 55 per person in the example) is a term that does not really have a “real life” meaning. We cannot directly observe someone and verify that their productivity is the number we have calculated.
· We have made up all the numbers! Because of this, usage of this equation becomes an exercise in the subjective judgment of the person calculating it, so ultimately the results will be whatever they want them to be.
The Economist’s Formula
There is a formula used in economics for various analyses called the Cobb-Douglas equation. This formula was used as a starting point in some academic research performed by Niringiye Aggrey, who studied labor productivity in three African countries.
 |
| Figure E |
Using this formula in the research results for Tanzania (the only one of the three countries studied that shows a positive contribution from management!), we can calculate a break-even analysis if we are willing to make assumptions about the input levels.
To perform this analysis, we make the following assumptions for use in the equation for our base case:
· Machinery Value = ²1 million
· Number of Employees = 100
· Manager Education Level = 16 years (i.e. Undergrad Degree)
· Proportion of Skilled Workers = 50% of workforce
· Workers Age = 40 years old
 |
| Figure F |
Before leaping to conclusions, we must remember that the benefit differentials resulting from this analysis must be reduced by the costs associated with each of them. Therefore, if the present value of the cost of the additional salary associated with a higher level of education in the Leadership scenario is greater than the cost of training 100 workers, then this will impact our conclusions.
The main benefit of this approach is that all the factors are observable. We can always calculate an average age, or education level, etc. of the various inputs. The output of the equation is also tangible - value of output divided by labor units.
The disadvantage of this approach is that the factors are very general. Is education level really the best proxy for leadership? Not all A-Players have the most education. Certainly if we ran this equation a few decades ago we might have missed the Leadership valued added differences for two software firms, where Microsoft would score lower because Bill Gates did not complete his undergraduate degree whereas a comparable competitor (IBM perhaps?) might have been run by an MBA graduate.
Another problematic aspect to notice is that this equation is specific to Tanzania. The results for Kenya and Uganda were quite different, such as the level of management education being a negative impact factor in the equation! In addition, the R-squared statistics of the study were in the 30’s, meaning that over 60% of the productivity differences between firms is outside of the factors under study. It is possible that both Individual Improvement items and Leadership items not considered may make a major contribution to that other 60%, or something else entirely.
Key Takeaways
While it is disappointing to not discover an acceptable formula, this in and of itself provides insight.
There is no conclusively best formula to use when considering our talent management efforts. In all likelihood this is due to the fact that we are dealing with people, who cannot be reduced to something so simplistic. Because each person is an individual, with their own mix of motivations, desires, histories, etc., there is no universal formula that will provide all the data we require to determine our approach.
For this reason, we need to keep an open mind – we must always consider different perspectives, models, and paradigms when considering the management of the organization, and use our best judgment and common sense in implementing whatever approach we have decided to select.
Questions
· What equations have you discovered that provide insight into talent management and its impact on the organization?
















