In Search of the Talent Equation

In reading “Talent Management Success: How A ‘Best to Work For’ Company Makes and Keeps Its Employees Happy” on Beth Miller’s Executive Velocity blog, I was intrigued by the fact that PBD, the company in question, sought to develop talent across their whole enterprise through a “best fit” process.

My interest came about because the approach depicted was applicable to all employees rather than what we might call “the chosen few”, which seems to be a talent management theme these days, encouraging organizations to focus on their “A-Players”, “High Potentials”, or “Superstars”.

The Problem with the “Chosen Few” Approach

Conceptually, there are some problems with the “chosen few” approach.

·       First, as noted in “5 Reasons NOT to Use the Olympics for Business Lessons”, any organization of a respectable size is quite unlikely to have an entire staff of these folks. If every company in the world is pursuing these folks, and A-players represent 5% of the workforce (if that), the odds are quite long that your firm will be the one they all gravitate towards.

·       Second, all employees notice when you are showering the bulk of the attention and other organizational goodies (training, promotions, recognitions, etc.) on a select minority, and this impacts morale, and ultimately you may find that your team has become the microcosm equivalent of “Occupy Wall Street”!

·       Third, if A-players represent 5% of our workforce, then it seems to me that their advantage needs to be really great in order to overcome efforts to develop the other 95%. If we can improve 95% of the people by 1%, then devoting our resources to the A-player crew needs to generate a return 19 times greater than that to break-even. Odds of 19:1 seem pretty long. Can their contribution really be that consistently great?

The Search Begins

The breakeven concept introduced in the third point above suggests that if we have an equation for employee talent that factors in both the employee and leader elements then we can analyze whether this 19 to 1 breakeven ratio is reasonable to assume.

For that reason we go looking for the Talent Equation.

The Knowledge Worker Formula

In “Wikifinance, Wikitreasury – Part 2“, an early Treasury Café post, we discussed that the Finance and Treasury role consists primarily of knowledge work. For this reason formulas related to knowledge worker productivity are of interest.

Figure A

Eric Mack proposes a formula for knowledge worker productivity as shown in Figure A. In this equation, knowledge, methodology and technology combine to create the knowledge worker’s productivity.

This is great from an “identify the important factor” viewpoint, but in terms of deploying this in practice several issues arise. What numbers are we to use? Let’s say all factors (i.e. M,T and K) are scored on a scale of 1 to 10. Then KWP would equal 1000 at its maximum, and 0 at its minimum. What does 1000 actually mean in terms of productivity? Five projects get done per day? Five per week? The results are not intuitive.

Another problem we face is that there does not appear to be any role for leadership or other management activities in the equation. M, T, and K can remain the same whether one has a great leader or a lousy one, and under this equation the worker will be equally productive under each. This makes the equation as it stands difficult to use for our break-even purposes.

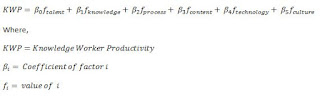Figure B

Figure B shows the Knowledge Worker Productivity equation proposed by the AKA Group. In this model productivity is the sum of a number of factors, each multiplied by factor specific variable.

A positive in this equation is that there are leader-related items such as culture and potentially process (depending on the process we are discussing).

However, if the meaning of numbers in the first KWP formula were not intuitive, in this equation it is even more problematic because each term has two numbers, the coefficient (the β item) and the value of the factor itself (the f item). How are these to be determined? And again, what is the value of the result?

Success and Talent Formulas

Striking out in the Knowledge Worker Productivity realm, we turn to more general models. A number of formulas seek to depict success or talent for anyone.

From FarrellWorlds, we have:

Success = Talent + Dedication + Passion + Luck

And from Nilofer Merchant:

S(uccess) = P(urpose)T(alent)^C(ulture)

As in the last section, these models are useful from the perspective of answering “what elements are important to consider” issues. However, for our break-even purposes these formulas share measurement problems - ask two people what “success” is and you will get two different answers.

The Per-Person Productivity Formula

One general model that holds a little more promise is one from Derek Irvine, who provides a formula that is heavy on management intervention:

Per-person productivity = Talent x (Relationship +Right Expectation + Recognition/Reward)

Talent is the individual employee’s factor, and the three terms in parentheses relate to the leadership functions.

Let’s assume that Talent is measured on a scale of 0 to 100. For the leadership factors, the critical number for the sum of these is 1. At points higher than this number, Per-Person Productivity improves from their base talent level. At points less than one, it declines.

Figure C

Figure C shows how this equation works under 3 different scenarios. The first column is the base case scenario, where the talent level is 50, and the leadership factors sum to 1.

The second column (II stands for “Individual Improvement”) is the scenario where we intervene by increasing everyone’s talent by 10%.

The final column (L stands for “Leader”) is the scenario where we improve the leadership factors by 10%, presumably by obtaining some of these A-Players.

The results of each intervention increase the firm’s total productivity from its base case level by 10%. This result is inherent in the equation, since both terms multiply together they will always increase the same percentage amount no matter which term you trigger.

However, what might result from this is that there might be a cost benefit factor which can be used to determine which approach is better. If the Individual Improvement action costs ²100 (for new readers, the symbol ² stands for Treasury Café Monetary Units, or TCMU’s, freely exchangeable at any rate into any currency you choose), then each unit of improvement cost us ²2.

In order to arrive at an “apples to apples” comparison, we need to be careful, as the concept of time enters into this analysis in two ways.

·       For the Individual Intervention scenario, if we assume the ²100 is a skills training cost, while this might be a one-time event,  its effects will not last forever since workers eventually move on to other positions, win the lottery, retire etc.

·       For the leadership scenario, we will need to pay our new A-Player a salary each and every year, so we need to factor in a stream of payments over time and relate that back to one single figure now.

Figure D

We do this via a Net Present Value (NPV) calculation. Figure D shows the results of this if we assume that the average worker tenure is 15 years, and we pay our A-Player ²10 more in year one than their B-player equivalent (i.e. the incremental increase, not total salary), and increase 3% thereafter. We ignore taxes and assume we have a cost of capital (pre-tax) of 10%.

Under these conditions, we are slightly better off going the A-Player route as the NPV is a little more than ²93, compared to ²100 for the Individual Improvement scenario.

While we successfully completed a break-even calculation using this equation, there are still 2 problems:

·       The output of the equation (e.g. 50 and 55 per person in the example) is a term that does not really have a “real life” meaning. We cannot directly observe someone and verify that their productivity is the number we have calculated.

·       We have made up all the numbers! Because of this, usage of this equation becomes an exercise in the subjective judgment of the person calculating it, so ultimately the results will be whatever they want them to be.

The Economist’s Formula

There is a formula used in economics for various analyses called the Cobb-Douglas equation. This formula was used as a starting point in some academic research performed by Niringiye Aggrey, who studied labor productivity in three African countries.

Figure E

After extensive transformation (such as using logarithms) and addition of variables (such as education level, years of experience, industry) to the basic formula, it ends up as that shown in Figure E.

Using this formula in the research results for Tanzania (the only one of the three countries studied that shows a positive contribution from management!), we can calculate a break-even analysis if we are willing to make assumptions about the input levels.

To perform this analysis, we make the following assumptions for use in the equation for our base case:

·         Machinery Value = ²1 million

·         Number of Employees = 100

·         Manager Education Level = 16 years (i.e. Undergrad Degree)

·         Proportion of Skilled Workers = 50% of workforce

·         Workers Age = 40 years old

Figure F

Figure F shows the result of this calculation, along with the results of our Individual Improvement scenario (represented by changing the Training variable) and the Leadership scenario (represented by increasing education level to 20 years – Masters or PhD level). In this case value is increased by about ²800,000 more through the Leadership scenario vs. the Individual Improvement scenario.

Before leaping to conclusions, we must remember that the benefit differentials resulting from this analysis must be reduced by the costs associated with each of them. Therefore, if the present value of the cost of the additional salary associated with a higher level of education in the Leadership scenario is greater than the cost of training 100 workers, then this will impact our conclusions.

The main benefit of this approach is that all the factors are observable. We can always calculate an average age, or education level, etc. of the various inputs. The output of the equation is also tangible - value of output divided by labor units.

The disadvantage of this approach is that the factors are very general. Is education level really the best proxy for leadership? Not all A-Players have the most education. Certainly if we ran this equation a few decades ago we might have missed the Leadership valued added differences for two software firms, where Microsoft would score lower because Bill Gates did not complete his undergraduate degree whereas a comparable competitor (IBM perhaps?) might have been run by an MBA graduate.

Another problematic aspect to notice is that this equation is specific to Tanzania. The results for Kenya and Uganda were quite different, such as the level of management education being a negative impact factor in the equation! In addition, the R-squared statistics of the study were in the 30’s, meaning that over 60% of the productivity differences between firms is outside of the factors under study. It is possible that both Individual Improvement items and Leadership items not considered may make a major contribution to that other 60%, or something else entirely.

Key Takeaways

While it is disappointing to not discover an acceptable formula, this in and of itself provides insight.

There is no conclusively best formula to use when considering our talent management efforts. In all likelihood this is due to the fact that we are dealing with people, who cannot be reduced to something so simplistic. Because each person is an individual, with their own mix of motivations, desires, histories, etc., there is no universal formula that will provide all the data we require to determine our approach.

For this reason, we need to keep an open mind – we must always consider different perspectives, models, and paradigms when considering the management of the organization, and use our best judgment and common sense in implementing whatever approach we have decided to select.

Questions

·         What equations have you discovered that provide insight into talent management and its impact on the organization?

Add to the discussion with your thoughts, comments, questions and feedback! Please share Treasury Café with others. Thank you!

This Strategic Control Map is Nuts!

There are several perspectives we can take on strategy.

One approach is to view our finance group as an independent business, and then deploy strategic tools to understand how to fulfill our mission and vision better (see for example “Rollin' the DICEE -Another Take on the Treasury Vision”). This is a helpful exercise that will lead to improved performance within our organization.

Another option is to take the overall organization’s perspective. This is important if finance is going to be a strategic contributor within the company. The strategic role of finance is becoming more and more important, as evidenced by books (such as “The Strategic Treasurer” and “Finance for Strategic Decision Making”), press articles, financial institution perspectives (“The Strategic Treasurer”), and top-tier finance and strategy firms assessments.

Finance is well-suited to play a strategic role due to the combination of core strengths in understanding value creation and analytics. Today we look at the Strategic Control Map, a tool to assist in strategy assessment and development.

What is the Strategic Control Map?

As discussed in our post on Return on Invested Capital, it is sometimes useful to break down an equation into separate sub-equations in order to understand some of the elemental drivers that produce the final result.

Figure A

The Strategic Control Map is a concept developed by McKinsey in the 90’s, and is essentially a visual representation of this “equation breakdown” process with respect to market capitalization.

Figure A shows the equation for Market Capitalization, which is simply the market value of a company’s equity and debt securities.

Figure B

By adding a numerator and denominator of the same term (meaning you are multiplying the original equation by 1, which does not change the result), we arrive at a breakdown of Market Capitalization into two components: Market to Book ratio, and Book Value. Figure B shows this representation.



Figure C

 The strategic control map can then be plotted with the Market to Book ratio on the y-axis and the book value on the x-axis (Figure C).

Enter Cost of Capital – Stage Right

The market to book ratio represents the market’s valuation of the firm’s investments compared to what those investments actually cost. This leads us to the concept of “excess returns”.

In finance, the phrase “excess returns” is used to describe a situation where the rate of return we earn from an investment is greater than our cost of capital.

Cost of capital represents what an investor needs to earn from an investment that carries a certain amount of risk.  Let’s look at two bonds to understand why.

Short-term US Treasury’s currently yield way less than 1%, due to the fact that they are low risk for two reasons. First, the US is a highly rated entity that has never defaulted on its obligations and has the ability to raise revenue on a large and wealthy economic base. Second, short-term debt is less risky than long-term debt because fewer things can go wrong in the next 6 months than could go wrong in the next 10 years.

On the opposite end, a 10-year Greek Bond has traded as high as 38%, because they are higher risk for reasons we have all heard about for years now. They have a weak economy and are burdening it excessively with funding demands, so there are little means to generate funds to pay off bonds. And there are a lot of things that can go wrong in Greece over 10 years compared to 6 months.

So an investor does not have one single required return. They have many different ones, and they are all related to the risk involved.  

·         Lower risk, lower return. A nice, safe, comfy short-term US Treasury? “I’m happy to make 1% on that”.

·         Higher risk, higher return. A risky 10-year Greek bond? “I need to make 38% to think about taking that one on”



Figure D

 Risk vs. Return is the basis for the cost of capital. Figure D shows this graphically. The more risk (which increases as we move along the x-axis) requires a higher return (which moves along the y-axis). Thus, the required rate of return is going to be an upward sloping line. For a given level of risk, move up the dashed line to find the required rate of return for that risk level, and notice that higher risk things require higher returns, and lower risk items require lower returns.

Enter Firm Investment – Stage Left

A company usually has a choice of several investments that it can make at any given time, sometimes referred to by cool names such as the “potential project portfolio” or “investment pipeline”.

For example, Farmer Joe’s Agricultural Empire might be considering any or all of the following investment possibilities: addition of a combine to accelerate harvesting, purchase of improved seed products, addition of a new grain silo, adding improved dryers to existing grain silos, etc.

Figure E

The investment possibilities will each have a different potential rate of return associated with them. Using the list above, maybe the combine is a 10% project, the seed products are 15%, the new silo is 12.5%, and the improved dryers is 20%.

The result of this fact is that the firm’s investment pipeline can be visualized as a downward sloping line, shown in Figure E, where the y-axis represents the rate of return (i.e. 20%, 15%, etc) and the x-axis is the project (combine, seeds, etc.).

Center Stage

So we have cost of capital entering from stage right, and the firm’s potential project portfolio entering from stage left, with the ultimate result that they meet at center stage.

This meeting is important. The firm’s investors expect a certain return on their investment given the risk level of the business. The firm has choices to make about which projects or investments to go forward with or turn down. The interplay informs the decision making.

Taking our example of Farmer Joe’s Agricultural Empire, if investors in this firm expect to make 10%, then Farmer Joe should undertake all 4 of the potential projects, as they all are expected to make this amount or more.



Figure F

 However, if Farmer Joe’s investors require 15% return based on the risk of the agriculture business, then Farmer Joe’s management should only invest in two projects, the seeds (15% return) and the dryers (20%). The other two projects, at 10% and 12.5%, do not earn enough to meet the investor’s required return.

We can depict this intersection by linking the two graphs we have previously seen together, with cost of capital providing the “connecting glue” between them. This is shown in Figure F.

The Market to Book Ratio Link

Now that we understand that a company makes decisions on various projects and opportunities that need to take into consideration the cost of capital, we can explore how this might work in the marketplace.

Case A: If we are a firm investing in 1 project that costs ²100 (for new readers, the symbol ² represents Treasury Café Monetary Units, or TCMU’s, freely exchangeable with any currency of your choice at any exchange rate you desire) and will return 20% forever after with no growth, then each year the firm will make ²20 in cash on this investment.

If the cost of capital for our firm is 10%, then using the simplified Dividend Discount Model (see “Apple’s Dividend – Good Financial Strategy?”) the market will value this investment at ²200 (20/10%). Our Market to Book ratio is therefore 2.

Case B: If we are a firm investing in 1 project that costs ²100 that will return 5% forever after with no growth, then this will generate cash each year of ²5.

If the cost of capital for our firm is 10%, then using the simplified Dividend Discount Model the market will value this at ²50 (5/10%), and our market to book ratio will therefore be 0.5 (50/100).  

Case C: If we are a firm investing in 1 project that costs ²100 that will return 10% forever after with no growth, then this will generate cash each year of ²10.

If the cost of capital for our firm is 10%, then using the simplified Dividend Discount Model the market will value this at ²100 (10/10%), and our market to book ratio will therefore be 1 (100/100).  

What we learn from these three cases is that if we earn our cost of capital then our Market to Book ratio will be 1, if we earn more than our cost of capital it will be greater than 1, and if we earn less than our cost of capital it will be less than 1.

Back to Strategic Control

Figure G

McKinsey breaks down the Strategic Control Map into 4 quadrants, as shown in Figure G. Companies in the upper left are in control, earning high returns on a large amount of investments. Companies in the bottom right are vulnerable, earning low returns on few investments. Companies in the upper right are considered vulnerable to takeover, given their smaller size but attractive returns. Companies in the bottom left need to focus on cost consolidation, as their large investment base needs to earn higher returns.

Figure H

In Figure H, we combine this quadrant view with our Project Portfolio line (shown in blue). This shows how difficult it is for a firm to be in strategic control, because there is a tension between earning high returns and making lots of investments.

From our example earlier, if Farmer Joe undertakes just its best investment, it will earn 20% and have a market to book ratio of 2. Few investments, high market to book ratio. This would place them in the upper left quadrant.

If they undertake all 4 projects (and if we assume equal value for each), they will average about 14% return, and their market to book will be about 1.4. Many investments, lower market to book ratio. This places them in the lower right quadrant.

To be in control a firm needs to find many, many high returning investments. Not so easy to do!

Using the Strategic Control Map

Figure I

For our Return on Invested Capital discussion, we used a local Chicago firm called John B. SanFilippo and Sons as our example. They are a producer of snacks such as peanuts, pecans, cashews, etc. sold under various brand names (hence this post’s title).

I looked up in Google Finance and Yahoo Finance their competitors, and created a strategic control map for this set of companies (using graphics in R). This is shown in Figure I.

Viewing this map, we can see several things.

·         First, there is one “big dog” and a bunch of “smaller dogs”.

·         Some firm’s are not earning their cost of capital (market to book below 1)

·         Evidence of the tension brought about by the Project Portfolio line is evident (higher returning firms are smaller in size)

·         Our friends at SanFilippo (JBSS in the graph) have some work to do

This last bullet I mention because if we overlay the Project Portfolio line into the graph, then the optimized tradeoffs should be on the line, so the line becomes the “most efficient frontier”.

Figure J

 We cannot be “upper and to the right” of the line because higher returning investments are not there.

Figure J shows the situation if we are “lower and to the left” of the line. In this case we are sub-optimal, we should either be earning higher returns on the investments we have made (the “earn more” direction) or be undertaking more investments at that particular rate of return (the “make more” direction).

Figure K

Figure K shows the Strategic Control Graph with the addition of what it looked like two years prior. The lines connect each firm’s current vs. previous position, indicating their progression over the past two years.

Several things stand out on this graph:

·         Our friends at SanFilippo have remained relatively constant, there is little movement within the two years

·         Both Lance (LNCE) and Diamond Nuts (DMND) exhibit movement consistent with the slope projected by the Project Portfolio line

·         Golden Enterprises (GLDC) and American Lorain (ALN) has seen their value reduced and have not grown

·         Inventure Foods (SNAK) has done something to dramatically increase the returns on its existing portfolio

From JBSS’s perspective, they need to either move to the right along the map or move upward. Given the distance traveling left to right between them and Diamond or Ralston (RAH), they would need to invest a lot of money in order to achieve this. It seems like it would be more likely that they be able to find a way to improve returns on their existing portfolio.

Alternatively, a merger with SNAK should move them up and to the right, which is the direction that you want to head on a Strategic Control Map.

From an industry perspective, it is possible that a merger between Lance and Diamond would move them to the right on the map. If they could combine this with improving returns on their product lines (either through synergies from the merger or better investment possibilities), they would be in a position to challenge Ralston for control within the industry.

Key Takeaways

The Strategic Control Map is one tool that can be used in a strategy setting to generate insights into industry performance and direction. Its usefulness is enhanced when we employ finance concepts into the analysis.

Questions

·         What does the Strategic Control Map suggest to you in the way of JBSS’s actions?

·         What insights for the industry do you notice from the Strategic Control Map?

Add to the discussion with your thoughts, comments, questions and feedback! Please share Treasury Café with others. Thank you!

Analytic Reminders You Can Learn From an 8-Year Old

My wife’s family is huge. She is one of eight, and many of her siblings have carried on this tradition in their families as well, the result being that her parents have over 30 grandkids.

This provides me ample opportunity to play all sorts of games. On our recent annual vacation to a camping cabin “resort” in the north woods of Minnesota (where cell phone reception is spotty at best), on one of those days when we are trapped indoors because the rain prevents any playground, beach, biking, fishing, or golf activities, I settled down to a game of Monopoly with an 8-year old.

The problem is…I should have been thinking more than I was.

Background

Monopoly is a board game that takes you around a square with 10 spaces on each side, for a total of 40 spaces in all. Most of the spaces represent “properties”, which you can buy and own, and when other players land on them you collect “rent” from them. Each turn you roll 2 dice and move your token accordingly. If you land on someone else’s property, you must pay them the rent for that property.

Most of the properties belong to color groups of 2 or 3. If you own all the properties in a color group, you have a “road”. When this occurs, you are able to invest in houses and hotels, which significantly increases the rental income you collect from other players. The only exception to this color group is the railroad and utility groups, which cannot be improved upon, though by owning more than one rental income increases.

It is only with a large amount of luck that you can obtain a road on your own movements. Because of this, at some point in the game players start to make trades – combinations of one or more properties and perhaps cash in exchange for others.

The Situation

After having traversed the board quite a few times, we arrived at the situation where all the properties were purchased but nobody owned a road. The 8-year old I was playing with proposed a trade, whereby I would give him the two railroads I owned (he owned the other 2) in exchange for Pacific Avenue, one of the three properties making up the “green” color group. Since I owned Pennsylvania Avenue and North Carolina Avenue (the other two greens), I would be in a position to build houses and hotels to increase my income while others would not.

Given the properties I held, it was also not possible for anyone else to get a road, so this trade appeared to me to be one where I would be able to slowly establish a juggernaut that all would succumb to.

Unfortunately for me, I did not take “Expected Value” into account, whereby my 8-year old opponent did (though maybe not consciously).

What is Expected Value?

Figure A

“Expected Value” is a term used in statistics and probability theory. It represents the "payoff" of a certain event multiplied by the probability of that event occurring. For a coin flip, this would be represented by the equation in Figure A.

For example, if I receive ²1 ( the symbol ² stands for Treasury Cafe Monetary Units, or TCMU's, freely exchangeable into any currency of your choosing at any exchange rate you desire) should a coin flip result in heads, and pay ²1 should the coin flip result in tails, given a 50/50 chance of each occurring, then my "Expected Value" is ²0 (.5 * 1 + .5 * (-1) = 0).

What if I receive ²1 on heads and pay ²0.50 on tails? Then my expected value is ²0.25 (.5 * 1 + .5 * (-.5) = 0.25).

What if I receive ²1 on heads and pay ²0 on tails? Then my expected value is ²0.50 (.5 * 1 + .5 * 0 = .5).

Figure B

More generally, the equations above can be represented by the formula in Figure B, which simply says for all events "i" whose probabilities total to 1, the expected value is the sum of the probability of that event occurring times the value of that event should it occur.

Applying Expected Value

Now that we understand expected value, we can apply this knowledge to my Monopoly trade with my 8-year old opponent.

The Monopoly board has 40 spaces, so if we assume that landing on each one is equally likely, then the probability of landing on each space is simply 1/40, or 0.025. After the trade, my opponent will have 4 railroad properties, each requiring a payment of 200 from the person landing on them. Using Formula B, they will have an expected value of 20 (.025 * 200 + .025 * 200 + .025 * 200 + .025 * 200 = 20).

I had the funds to put up one house on my green properties. Those landing on green properties with one house need to pay rent of 130 for two of the three and 150 for the other. Thus, my expected value, using the formula in Figure B, is 11.5 (.025 * 130 + .025 * 130 + .025 * 150 = 10.25).

Since we were playing each other, my opponents expected value is also my expected payment, and vice versa. Unfortunately for me, this means that I can expect to pay 20 while receiving only 10.25, and thus my net expected value is -9.75. Because of this, the possibility of amassing enough cash to buy another round of houses for my green properties (which would require 450) is quite unlikely. If I could achieve this, it would put me in a positive position, as the expected value with two houses is 30.75 (0.25 * 390 + 0.25 * 390 + 0.25 * 450 = 30.75).

The lesson from this basic analysis was that in order for me to make the trade, I needed enough cash on hand to build two rounds of houses on the green properties immediately in order to make a positive expected value. Lacking that, I should not have made the trade.

Path Dependence

Since movement in Monopoly is governed by the roll of 2 die, the 1/40 probability assumption we used in the last section is somewhat inaccurate. If our token is on the Board in space #1, then it is more likely that on the next roll we will land on space #8 (i.e. rolling a 7) rather than space #3 (i.e rolling a 2), so each of these spaces have different probabilities (the odds of a 7 are 7/36, while those of a 2 are 1/36).

Similarly, on the next turn, the probabilities of different properties being landed on will depend on where we landed the turn before. Had we rolled a 2 last time and moved to space #3, on our next turn it is now more likely we will land on space #10 (rolling a 7) instead of space #15 (rolling a 12).

This concept, that the future outcome is determined by the past, is known by the term “path dependence”.

A Trip to Monte-Carlo

One solution to estimating results in a path dependent situation is to perform a Monte-Carlo simulation. Monte-Carlo models use statistically based random numbers to project the future over and over. By doing this, we can develop an estimate of the probabilities of events we are concerned about occurring.

In order to accomplish the simulation, we program the movement process around the Monopoly board, taking into account the die roll (in this setting the random element of the Monte Carlo), and the game elements that impact position (e.g. the “Go to Jail” space, Chance and Community Chest cards, etc.). This was done using a combination of Excel and Visual Basic for Applications (I am happy to email this spreadsheet and code to you if you’d like, simply connect with me on LinkedIn and provide me an email address).

We then simulate 1,000 games from every one of the 40 possible starting positions. In each simulation, all players had to go around the board at least 5 times. This results in 40,000 data elements to analyze.

Evaluating the Data

Figure C

For the analysis portion, we import the results into R (an open-source statistical program). I prefer R to Excel for this phase as it is in more robust in handling the data and offers a wider variety of analysis and graphics options (I could have set up the Monte Carlo in R, but selfishly wanted to practice my VBA skills).

The t-test is a statistical metric that determines whether the average of one set of data is significantly different (meaning likelihood is set to a high threshold, such as less than 5% chance) than the average of another set. Figure C shows the formula for a t-test statistic for equal sample sizes with an assumed equal variance.

One thing I like to do as an analyst is verify that my understanding of equations is sound and that the programs I am using are performing calculations according to that understanding. For that reason, I calculated in Excel the t statistic for the test between Expected Value results for starting position #1 and starting position #16 (Figure D), and then compared that to the R output (Figure E).

Figure D

Once the t-statistic is calculated, it compared to a table (which is based on the number of observations) that determine its “p-value”. The p-value represents the probability that the results are from the same data set (the “null hypothesis”). If the p-value is very low, this means that there is only a slight chance the data are the same, or in other words it is likely the data are from “different” value distributions.

Figure E

Figure F

Figure F shows the p-values for the average Expected Value of landing on the green properties from three positions – Go, Pennsylvania Railroad, and Pennsylvania Avenue compared to all the other starting positions. The black line at the bottom is the .05 p-value threshold. Items below this line are significantly different (notice also that the p-value is 1 in spots where the distribution is comparing results to itself, remembering that the p-value is a measure of the likelihood the data are from the same distribution).

Looking at the orange line (starting position is “Go”, space #1), there is not a significant difference in Expected Values for this position vs. its near neighbors (up to around space #10, and space #30 and up) but is significantly different from Expected Values in the 10’s and 20’s.

Conversely, the brown line (starting position “Pennsylvania Railroad”, space #16) shows no significant difference between its near neighbors but significant difference from starting spaces further away (spaces #1-#10 and #30 +).

This process confirms the path dependency of Expected Value, they are different depending on where you start are on the board.

Figure G

However, now let’s take a look at Figure G. The Expected Value of each of the starting positions is around 10, and the range is not very great. The lowest expected value is 9.51 and the highest is 10.90. So even though they are significantly different in the statistical sense, the difference is not really great enough to change the value of the Railroad for Green Properties trade with the 8-year old.

The mean of the Expected Values in Figure G is 10.18, surprisingly close to our initial pass estimate of 10.25. So while path dependence does occur in the game, in this case it is not great enough to affect the outcome over a simpler set of assumptions.

Finally, I looked at the number of times the simulation resulted in a higher expected value for my side of the trade vs. that of my 8-year old opponent. On average, across all starting positions, only 13% of the time did I come out ahead (ranging between 10% and 16% depending on starting position). Based on this, I was very unlikely to win the game.

Conclusion

My failure to utilize the tool of Expected Value cost me the game. Sitting in a cabin near a lake in the woods is not the first place one might think to utilize analytical tools, however, in this case it would have helped.

The tools we have learned and deploy can often be used in more settings than we might think, so long as we are willing to be a little creative with them.

Next time I play that kid I might bring my computer!

Key Takeaways

Calculating Expected Value is a tool that can be used to assess alternative situations in order to inform decisions about what to do or not. Through the use of Monte Carlo simulation, even situations involving path dependent factors can utilize the Expected Value tool. As always, judgment needs to be utilized in assessing data and output of these calculations.

Questions

·         Have you encountered game situations where statistical concepts have been useful?

·         How have you deployed analytic tools in unusual situations or settings?

Add to the discussion with your thoughts, comments, questions and feedback! Please share Treasury Café with others. Thank you!